Oleh :

  Tengku Zawawi bin Tengku Zainal

Unit Matematik MPKTBR

Kuasa dua dan punca kuasa dua adalah antara tajuk yang sukar di peringkat menengah rendah. Strategi pengajaran dan pembelajaran tajuk berkenaan, banyak tertumpu kepada kaedah hafalan di samping pendedahan , dan kemahiran menggunakan buku sifir serta kalkulator eletronik. Para pelajar hanya mengetahui bahawa; punca kuasa dua adalah songsangan bagi kuasa dua, dan begitulah sebaliknya, kuasa dua adalah songsangan bagi punca kuasa dua. Penggunaan simbol yang ‘archaic’ seperti Ö dan istilah yang tidak tekal ( seperti ‘kuasa’ dan ‘punca’ ), telah menambahkan lagi kesukaran dan kekeliruan di kalangan pelajar ( Harkin and Rising, 1974 ; Ngean, 1984 ). Amat jarang guru menggunakan kaedah-kaedah pengajaran matematik yang lebih menarik dan bermakna seperti kaedah penemuan, untuk mengajar topik-topik yang sukar seperti kuasa dan punca kuasa dua. Pengajaran dan pembelajaran yang bermakna bukan sahaja dapat membantu pelajar membina skim pengetahuan yang betul, malah dapat menimbulkan rasa minat dan cinta terhadap matematik.

Perkataan ‘root’ berasal daripada bahasa Arab, ‘al-jadhar’ , yang kemudian diterjemahkan kepada bahasa Latin menjadi ‘radix’ ( Al-Daffa’, 1977 ). Menurut istilah ahli aljabar Islam, al-jadhar mempunyai dua pengertian: anu ( al-majhul ) atau punca kuasa dua ( al-tajdhir ) . Hakikatnya, kedua-dua pengertian ini membawa maksud yang sama iaitu mencari penyelesaian suatu persamaan ( Mat Rofa, 1995 ). Anu digunakan untuk penyelesaian ( dipanggil punca ) bagi persamaan yang umum sedangkan al-tajdhir dikhususkan untuk penyelesaian persamaan;

x² = a , a ialah integer positif

Ibnu Al-Banna’ mentakrifkan punca kuasa dua a ialah suatu nombor x yang memenuhi persamaan di atas; x kadang-kadang disebut oleh ahli geometri sebagai dil’ yang bermaksud sempadan segiempat sama dengan keluasaan a.

Pada peringkat awal, punca kuasa dua dirumus dan disebut keseluruhannya secara lisan sebagai ‘Radix two’ atau ‘The root two’. Simbol yang mula ditemui ialah Ö ( disebut ‘punca kuasa dua ‘). Kemudian bertukar kepada simbol Ö · dan seterusnya kepada simbol , sehinggalah sekarang ( Harkin and Rising, 1974 ). Simbol ini adalah sebahagian daripada budaya intelektual semasa zaman kebangkitan yang barangkali tidak sesuai dengan budaya intelektual pada hari ini.

Al-Karkhi, se orang ahli matematik Islam, telah mengemukakan cara menganggar nilai punca kuasa dua dengan menggunakan formula ( Al-Daffa’ , 1977 ; Shauqi dan Al-Daffa’, 1985 ) :

Terdapat beberapa rumus lain yang telah dikemukakan oleh tokoh matematik Islam , seperti :

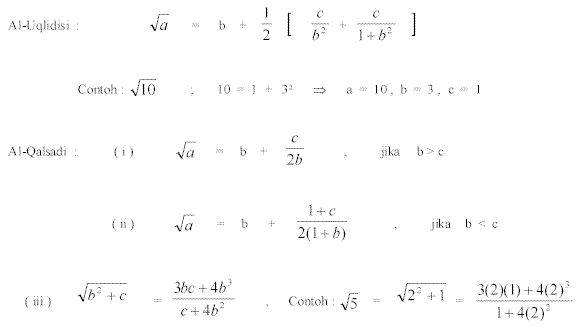
( Shauqi dan Al-Daffa’, 1985: 111 - 116 )

Sekurang-kurangnya terdapat dua pendekatan yang berbeza untuk menemui punca kuasa dua. Pendekatan pertama ialah dengan mengenalpasti pola, dan pendekatan kedua ialah dengan menggunakan kaedah algebra. Kedua-dua pendekatan ini menggunakan konsep yang berbeza tapi sama algoritma ( Edge, 1987 ). Dalam ruangan ini, hanya pendekatan pertama dikemukakan iaitu dengan cara mengenalpasti pola.

1² = 1 = 1

2² = 4 = 1 + 3

3² = 9 = 1 + 3 + 5

4² = 16 = 1 + 3 + 5 + 7

5² = 25 = 1 + 3 + 5 + 7 + 9

Ini menunjukkan bahawa :

1² bersamaan dengan jumlah satu nombor ganjil yang pertama

2² bersamaan dengan jumlah dua nombor ganjil yang pertama

3² bersamaan dengan jumlah tiga nombor ganjil yang pertama

4² bersamaan dengan jumlah empat nombor ganjil yang pertama

5² bersamaan dengan jumlah lima nombor ganjil yang pertama

Seterusnya boleh dibuat kesimpulan :

Oleh kerana dengan menambah nombor ganjil berturut-turut kita perolehi nombor kuasa dua, maka dengan menolak nombor ganjil berturut-turut kita akan perolehi punca kuasa dua.

Contoh :

Kita telah menolak enam nombor ganjil berturut-turut daripada 36 sehingga nilainya bersamaan sifar, maka:

Jika kita memeriksa nombor ganjil, kita akan temui :

Nombor ganjil pertama , 1 = 2 ( 0 ) + 1

Nombor ganjil kedua , 3 = 2 ( 1 ) + 1

Nombor ganjil ketiga , 5 = 2 ( 2 ) + 1

Nombor ganjil keempat , 7 = 2 ( 3 ) + 1

Nombor ganjil kelima , 9 = 2 ( 4 ) + 1

Seterusnya :

Nombor ganjil kesepuluh = 2 ( 9 ) + 1 = 19

Nombor ganjil keempat puluh satu = 2 ( 40 ) + 1 = 81

Ini akan memendekkan jalan kerja bagi nombor yang besar.

Contoh 1: Ö 121

Þ Ö 121 = 11

Kita sudah pun mengetahui bahawa 10² = 100 ; jadi menolak 100 adalah bersamaan dengan menolak 10² iaitu jumlah 10 nombor ganjil yang pertama :

Kita mesti ingat bahawa nombor ganjil yang berikutnya ialah yang ke 11 iaitu : 2 ( 10 ) + 1 = 21

Sekali lagi kita perolehi : Ö 121 = 11

Contoh 2 : Ö 484

Þ Ö 484 = 22

Contoh 3 : Ö 1089

Þ Ö 1089 = 33

Contoh 4 : Ö 729

Þ Ö 729 = 27

Jika diperhatikan contoh-contoh di atas, satu lagi generalisasi boleh dibuat :

[ Dalam contoh 3 ] : 61 + 63 + 65 = 189

[ Dalam contoh 4 ] : 41 + 43 + 45 + 47 + 49 + 51 + 53 = 329

Secara amnya :

Maka penyelesaian bagi Contoh 4 boleh diringkas :

Þ Ö 729 = 27

Contoh 5 : Ö 1156

Contoh 6 : Ö 784

Contoh : Ö 676

Þ Ö 676 = 26

Penggunaan kaedah di atas boleh dikembangkan kepada contoh-contoh yang melibatkan bilangan digit melebihi 5, dan nombor perpuluhan. Al-Uqlidisi, Al-Khawarizmi, dan Ibnu Al-Banna ( dalam Mat Rofa, 1995 : 61 - 70 ) juga turut menyumbangkan idea melalui contoh-contoh yang menarik bagi mencari nilai punca kuasa dua. Kaedah-kaedah yang digunakan dalam contoh-contoh di atas dipercayai berasal daripada idea dan penulisan tokoh-tokoh tersebut.

Ali Abdullah Al-Daffa’ (1977). The Muslim Contribution to Mathematics. Humanities. London

Edge, J. (1985). " Square Roots ". Mathematics in School. V4(2) : 7-9

Harkin, J. B. and Rising, G. R. (1974). " Some Psychological and Pedagogical Aspects of Mathematics

Symbolism". Educational Studies in Mathematics. Vol. 5 : 255 - 260.

Jalal Shauqi dan Ali Abdullah Al-Daffa’ (1985).al-‘Ulum al-Riyadhiyyat fil-Hadharah al-Islamiyyah Juz. 1.

Dar Jun.

Mat Rofa Ismail (1995). Sejarah Aritmetik Dan Aljabar Islam. UPM

Ng, See Ngean (1984). " Pengajaran dan Pembelajaran Matematik Sekolah Menengah Di Malaysia ". Dalam

Shahrir Mohd Zain. Dasar dan Peranan Pendidikan Matematik Di Malaysia . Bangi. UKM : 29 - 40